Arena Experiment, in 15 Minutes: What Actually Works for LLM Evals
This is the plain‑English summary of our full technical post benchmarking 14 estimators on 5k Chatbot Arena prompts. If you want the math, proofs, and all ablations, read the long version; this page is for quickly deciding how to evaluate your models in practice.
TL;DR
- Cheap judges can replace most expensive labels—if you calibrate them against a small "oracle" slice.
- On shared prompts, generate fresh responses and use Direct + two‑stage calibration. It hits 94% pairwise ranking accuracy (averaged across regimes) and avoids fragile propensity tricks.
- Off‑policy IPS fails with teacher forcing (ranking ≈ random); Doubly Robust + stabilized weights recovers strong performance but costs more.
- Always calibrate judge scores (don't trust raw judge numbers). Add response length as a covariate—ranking improves across the board.
- Show honest error bars. Our uncertainty accounting includes the fact that the calibrator itself is learned (not fixed).
The three measurement tasks
Most AI evaluation focuses narrowly on ranking—identifying which model is best. But production deployment requires answering three related questions. All three estimate the same thing: V(π) = expected oracle outcome under policy π. What differs is how we evaluate success.
What's a "policy"? A policy π is a complete generation configuration: model (e.g., Llama 3.3 70B), system prompt, decoding parameters (temperature, top-p), and any post-processing. The goal is to estimate V(π)—the expected oracle outcome under that policy.
1. Ranking
Which policy is best? Can we reliably order variants by quality? This is the traditional focus of model evaluation and leaderboards.
Evaluation:
Correct ordering. Metrics: pairwise accuracy, top-1 accuracy, Kendall's τ.
2. Magnitude
What's the actual policy value? If we deploy this variant, what conversion rate / user satisfaction / revenue can we expect?
Evaluation:
Accurate point estimates of V(π). Metric: RMSEd (oracle-noise-debiased RMSE).
3. Uncertainty
How confident are we? How many samples do we need? Uncertainty quantification enables efficient resource allocation.
Evaluation:
Valid statistical inference on V(π). Metric: 95% CI coverage rate (should be ≈95%).
Why we ran this
Evaluating LLMs on outcomes that actually matter—human preference, conversion, revenue—gets expensive fast. Most teams therefore use "LLM‑as‑a‑judge" as a proxy. The practical question is: with a small amount of expensive oracle truth, which estimators let us trust proxy‑based evaluations across all three measurement tasks?
What we did (the short version)
- Data: 5,000 real prompts from Chatbot Arena (first‑turn English), used for all policies (paired design).
- Policies: Five Llama configurations: base, clone (A/A), parallel_universe_prompt, premium (bigger model), and an adversarial unhelpful.
- Labels: Each response gets a cheap judge score (GPT‑4.1‑nano) and an oracle label (GPT‑5). We also study the realistic case where only 5–50% have oracle labels.
- Estimators: 14 methods across three families—Direct (fresh responses), Importance Sampling (reuse logs), and Doubly Robust (combine both).
- Costs (Oct 2025 ballpark): Judge calls are ~16× cheaper than oracle calls; calibration lets you use mostly judge scores while staying on the oracle scale.
Setup: Judges, Oracles, and Score Types
Judge scores: CJE works with direct scores (0–100 ratings) or pairwise comparisons (A vs. B wins—convert to continuous scores via Bradley‑Terry). This experiment used direct GPT-4.1-nano ratings, calibrated to GPT-5 oracle scores.
Oracle (Y) vs. Idealized Oracle (Y*): We use GPT-5 as the oracle Y (expensive, high-quality labels)—the highest practical rung we can reach at scale. The true target—Y* (Idealized Deliberation Oracle)—would be what infinite deliberation concludes about quality.
GPT-5 is closer to Y* than GPT-4.1-nano, but it's still a surrogate (model biases, finite reasoning). For production: use the highest practical rung available as Y—human judgments, A/B test outcomes, expert audits, or whatever represents your best signal. This experiment demonstrates the methodology; you'd swap GPT-5 for your actual oracle.
Key idea—CJE in one paragraph: Learn a mapping from cheap judge scores to the oracle scale using a small labeled slice, then apply it to lots of judge scores. Estimate policy values and produce uncertainty that includes both sampling noise and "we learned the calibrator" noise. If that mapping transports across policies/time, you can evaluate many systems cheaply and reliably.
The core assumption: Your judge (surrogate) must be predictive of the oracle outcome, even if it's biased. Example: a judge that prefers verbosity can still work—calibration learns "score 8 with 200 tokens ≈ oracle 0.65" vs "score 8 with 50 tokens ≈ oracle 0.75." But a judge that's uncorrelated with the oracle (random noise) can't be calibrated. Check correlation > 0.3 as a floor; > 0.6 is comfortable.
The CJE Workflow
The punchline results (no equations)
| Method | Pairwise % | Top-1 % | Kendall's τ | Verdict |
|---|---|---|---|---|
| Direct + two‑stage + cov (aka direct+cov) | 94.3% | 89.4% | 0.887 | ✅ Best default |
| DR + SIMCal‑W + cov (aka calibrated‑dr‑cpo+cov) | 94.1% | 87.5% | 0.881 | ✅ For log reuse |
| Stacked‑DR + cov (aka stacked‑dr+cov) | 91.9% | 84.7% | 0.842 | Strong alternative |
| SNIPS (raw IPS) | 38.3% | 8.7% | -0.235 | ❌ Avoid |
| Calibrated‑IPS (aka calibrated‑ips) | 55.6% | 20.0% | -0.061 | ⚠️ Still fails |
Results averaged across all experimental regimes: 5 oracle coverages (5%, 10%, 25%, 50%, 100%), 5 sample sizes (250, 500, 1K, 2.5K, 5K), and 50 seeds. "Random" baseline ≈ 50% pairwise, 20% top‑1, τ ≈ 0.
Ranking metrics exclude the adversarial unhelpful policy (by design, it breaks transportability).
What CJE returns: estimates with honest uncertainty
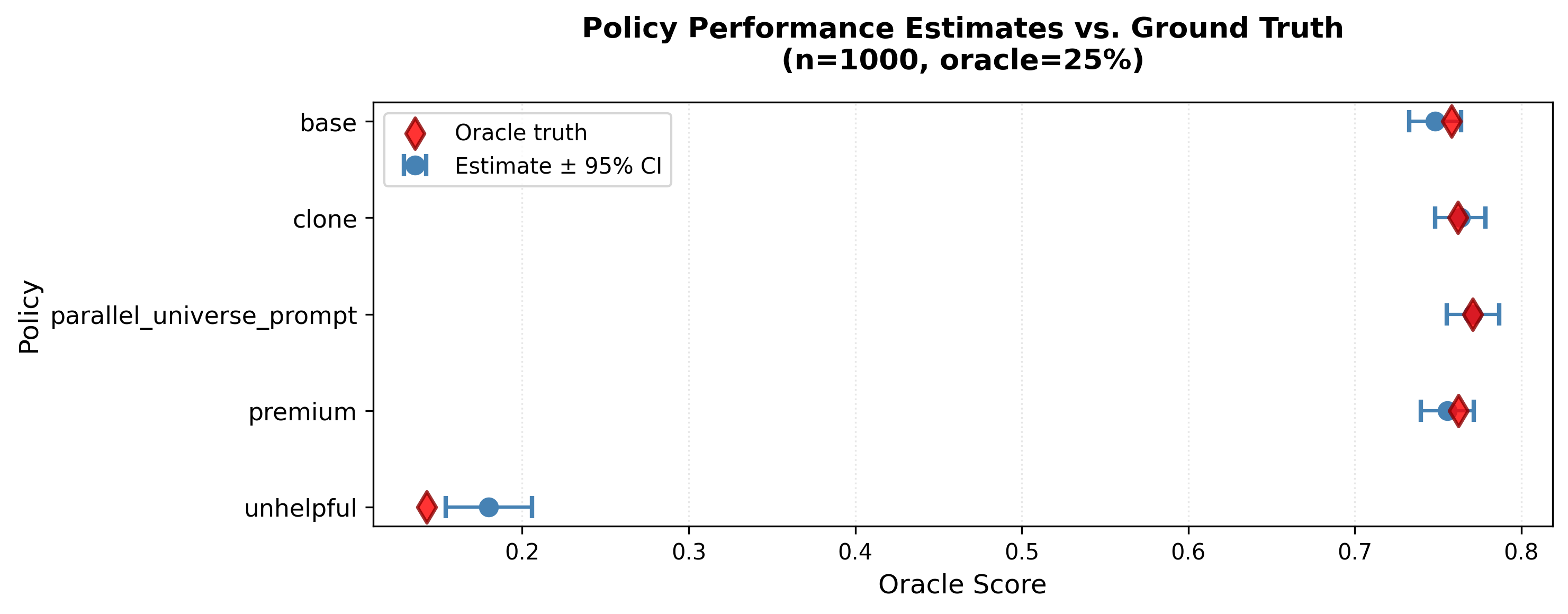
Example output: CJE estimates (blue circles with error bars) closely match oracle ground truth (red diamonds). With n=1,000 evaluations and only 25% oracle labels, the 95% confidence intervals successfully cover the true values. This is what you get when you run the Direct method—not just point estimates, but calibrated uncertainties that reflect both sampling noise and calibration uncertainty.
Key takeaways:
- ✅ Direct + two-stage calibration is the best default: Simple, fast, no teacher forcing, 94% pairwise accuracy.
- ❌ Plain IPS fails catastrophically: Worse than random (38% pairwise vs 50% baseline) due to weight degeneracy. With poor overlap, effective n drops from 5000 to ~30. Rankings invert.
- ✅ DR + stabilized weights recovers: Matches Direct performance but costs 7× more runtime.
- ✅ Always calibrate: Raw judge scores give 0% CI coverage (error bars lie).
- ✅ Add response length: Typically adds +5–7 pp top‑1 for Direct and DR methods (smaller gains for stacked estimators).
What to use, when
If you can generate fresh responses
Use: Direct + two‑stage calibration
Simpler, faster, and more reliable than logs‑only methods. Covers most offline benchmarking and model selection tasks.
If you must reuse logs
Use: Doubly Robust + stabilized weights
Only if there's decent overlap (ESS > 0.1×n) and you can compute propensities reliably via teacher forcing.
Other scenarios
📝 Multi-turn conversations or agent traces
Approach: Assign judge + oracle scores at the trajectory level (full conversation or task completion). Use Direct method on paired trajectories across policies. Teacher forcing propensities become intractable for multi-turn; stick with fresh generation.
⚡ Evaluating many policies quickly (>10 candidates)
Approach: Generate fresh responses on a shared prompt set (1k–2.5k). Judge all responses, collect oracle labels on base policy only (25% coverage). Calibrate once, apply to all candidates. Check transportability diagnostics; if any policy fails, add 50–100 oracle labels from that policy and recalibrate with pooled data.
🚫 Weak overlap in logs (ESS < 0.05×n)
Reality check: No off-policy estimator will save you. Even DR + stabilized weights will have massive variance. Either (1) generate a small fresh draw (n=500–1k) and use Direct, or (2) accept that you can't reliably evaluate this policy from historical logs—treat it as exploratory only.
How much data do you need?
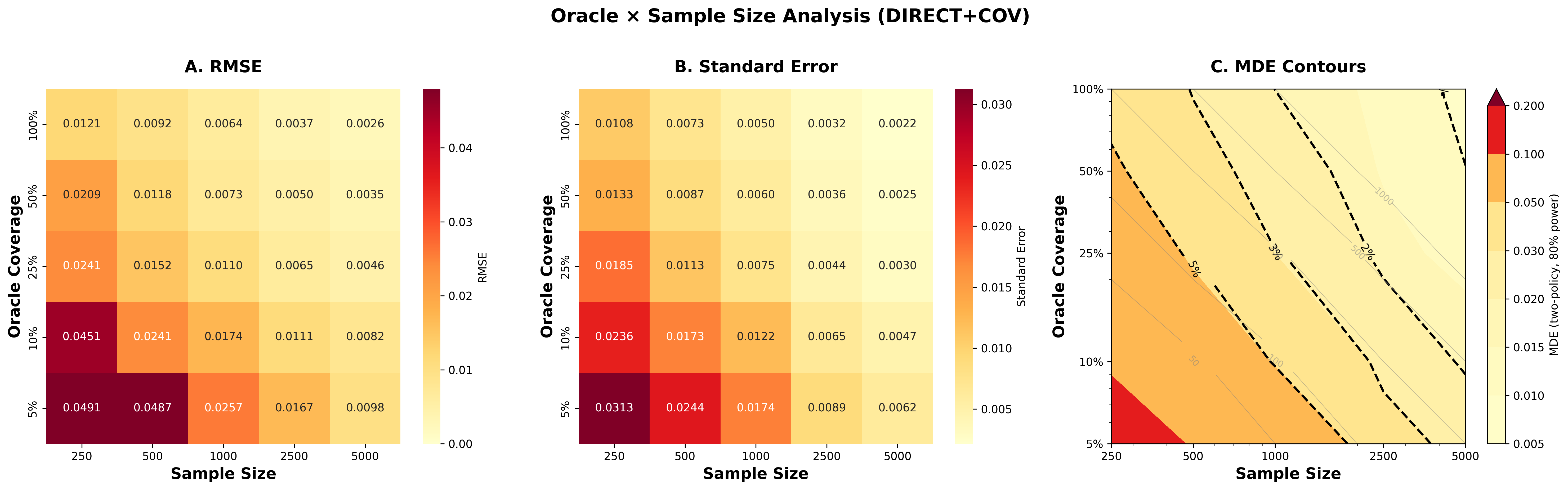
Power analysis for Direct+cov: Panel A shows RMSE decreasing with sample size and oracle coverage. Panel B shows standard errors. Panel C shows MDE contour lines—with n=1000 and 25% oracle coverage, you can detect ~2% effects. Click to enlarge.
For ranking policies
Usually sufficient for solid policy ordering
For detecting small effects (<1%)
Needed for tight confidence intervals
Oracle coverage regime guide
⚠️ Why honest uncertainty (OUA) matters
Standard methods treat the calibrator as fixed—as if the judge→oracle mapping were known with certainty. That's wrong: you learned it from a finite sample, so there's uncertainty in the mapping itself.
Concrete impact: Without OUA, nominal 95% confidence intervals only achieve ~65% actual coverage in our experiment (they're too narrow). OUA widens the intervals to be honest. If oracle coverage is only 5–10%, calibration uncertainty can dominate—you'll see wider CIs, but they'll actually cover 95% of the time. Better wide and truthful than tight and wrong.
When this breaks: Concrete failure modes
Transportability Failure: The "Unhelpful" Policy
What happens: You calibrate the judge→oracle mapping using typical policies (base, premium, etc.). Then you evaluate an adversarial "unhelpful" policy that produces terrible responses. The transportability test fails: mean residual = -0.312, p < 0.001.
Why: The calibrator learned the S→Y relationship in the "good response" range. The adversarial policy produces responses so bad they're outside the calibration range—extrapolation failure. Rankings still work (it's correctly identified as worst), but point estimates are systematically biased.
Fix: Add 50–100 oracle labels from the adversarial policy, recalibrate with pooled data. The transportability diagnostic (residual plot by policy) catches this automatically.
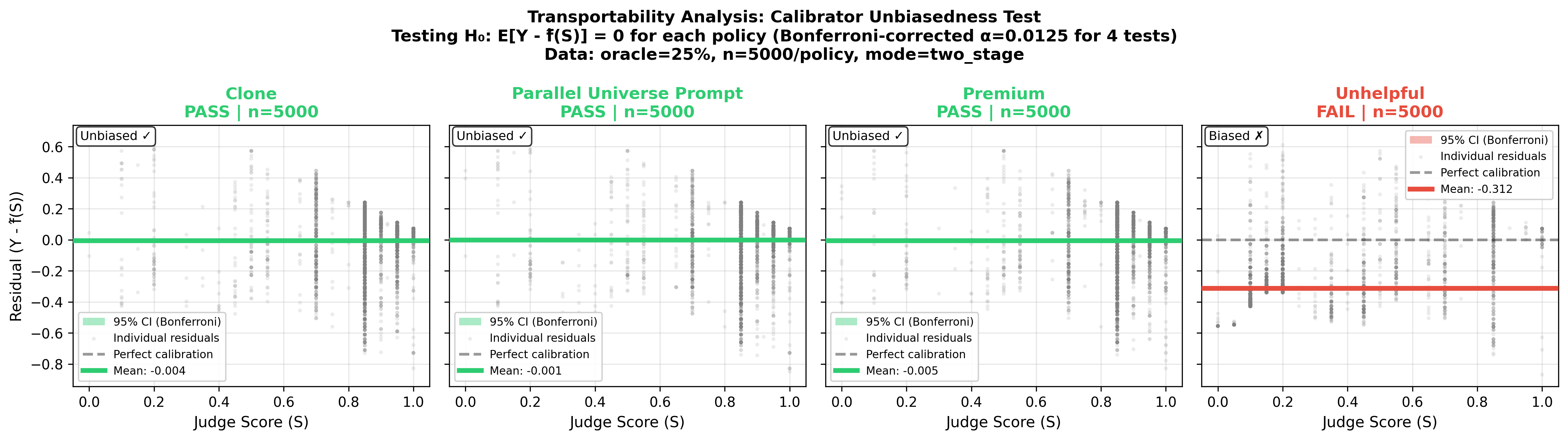
From the experiment: Testing H₀: E[Y - f(S, X)] = 0 for each policy (Bonferroni-corrected α=0.0125 per policy). Clone, Parallel Universe, and Premium pass—calibration transports cleanly. Unhelpful fails—the mapping learned from base systematically underestimates oracle scores for adversarial responses. This is why we exclude it from ranking metrics (by design, it breaks transportability).
Temporal Drift
What happens: You calibrate in January. By April, user preferences have shifted (more emphasis on conciseness). Your judge→oracle mapping is stale; estimates drift off.
Why: The oracle (user preferences) changed, but your calibration assumed they were fixed.
Fix: Run transportability diagnostics monthly on recent data. If residuals trend non-zero, refresh calibration with 200–500 new labels.
IPS Weight Degeneracy
What happens: You use raw SNIPS on logged data. Rankings are worse than random (38% pairwise accuracy; random = 50%). One policy gets all the weight; the rest are ignored.
Why: Poor overlap + teacher forcing noise → a few samples dominate the effective sample size. With n=5000, ESS drops to ~30.
Fix: Use DR + stabilized weights (SIMCal-W) or switch to Direct method if you can generate fresh responses. Never use raw IPS for ranking.
Practical, step‑by‑step (do this)
- Pick a shared prompt set (1–5k typical). Generate responses from each policy you want to compare.
- Score everything with a cheap judge (fast LLM or heuristic).
- Collect oracle labels for a slice (start with 25%; go lower later if diagnostics look clean).
- Run Direct + two‑stage calibration (judge→oracle with response length as a covariate).
- Report point estimates + 95% CIs that include calibration uncertainty. Add pairwise accuracy / Kendall's τ for ranking.
- Check transportability diagnostics (residuals by policy). If they fail, recalibrate or expand covariates.
Where Doubly Robust fits
DR is your "belt‑and‑suspenders" option for log reuse: even if propensities are imperfect, a good outcome model (the "critic") corrects most of the bias, and stabilized weights clean up the rest. Use it when:
- You really need to reuse a large log from a single policy ("logger").
- You can compute propensities with teacher forcing (and you trust the implementation).
- You can afford some fresh draws to help the critic generalize.
If overlap is weak (weights explode; effective sample size tiny), no estimator will save you—collect fresh responses and use Direct.
Humans vs models as the oracle
We used GPT‑5 as the oracle to stress‑test methods cheaply. The workflow is the same with human labels: calibrate judge→human, include rater noise in the error bars, and periodically re‑check transportability. If your real goal is human impact, calibrate against a small human slice and keep model‑judged scores for scale.
Recommended defaults
Estimator
Direct + two‑stage calibration (length‑aware)
DR + stabilized weights only if you must reuse logs
Data
Start with 1–2.5k prompts, 25% oracle
Lower oracle % later if diagnostics stay clean
Reporting
Point estimates + 95% CIs with calibration uncertainty
+ ranking metrics + transportability checks
Limitations to keep in mind
- GPT-5 as oracle ≠ human preferences. We used GPT-5 to stress-test methods cheaply and at scale. The workflow is identical with human labels, but if your goal is predicting human impact, calibrate against a human slice (not just model judgments). Model-as-judge and model-as-oracle can share systematic biases (verbosity, style, safety theater) that humans don't.
- Domain specificity. Sample size and oracle coverage recommendations are specific to this prompt distribution, judge-oracle correlation (~0.73), and effect size regime. Your domain may differ—run your first analysis with more oracle coverage than you think you need, then use diagnostics to find your optimal design.
- Teacher forcing brittleness. Off-policy propensities (for IPS/DR) depend on accurate teacher forcing implementation. Small bugs (wrong tokenization, incorrect logprob extraction) can silently destroy overlap. Always validate ESS > 0.1×n before trusting off-policy estimates.
- Transportability is an assumption, not a guarantee. The judge→oracle mapping may shift across policies or time. Run residual diagnostics on every new policy; refresh calibration monthly for deployed systems. When diagnostics fail, recalibrate—don't blindly trust old mappings.
✓ Fast checklist
If no, recalibrate or add covariates
Want more?
Conceptual foundations
This experiment instantiates the surrogacy framework—treating GPT-4.1-nano as a surrogate S, GPT-5 as the operational oracle Y, and using AutoCal-R to learn the calibration mapping.
For the theory of why this works and how to extend it to human outcomes, start with AI Quality as Surrogacy.
Full technical details
The complete Arena Experiment post includes all ablations, estimator definitions, uncertainty math, diagnostics, and reproducible code.
Software: pip install cje-eval · CLI: python -m cje.interface.cli --help · Examples: GitHub examples