Canonical Reference
CIMO Glossary & Foundational Theory
The single source of truth for notation, assumptions, and core concepts. This document defines the axioms that prevent the "Is-Ought" fallacy in AI evaluation.
Canonical Authority
This glossary is the canonical reference for all CIMO documentation. In the event of a conflict between this document and a blog post or technical appendix, these definitions take precedence.
Production
Battle-tested, empirically validated
1. The Causal Chain of Measurement
The fundamental premise of the CIMO Framework is that we cannot measure welfare directly. We must construct a causal chain that links cheap signals to idealized outcomes.
S → Calibration (f) → Y → Bridge (A0) → Y*
The CIMO Framework transforms cheap signals into validated welfare estimates
- S (Surrogate)
- The raw signal. Cheap, abundant, noisy. Examples: LLM judge score, BLEU, perplexity.
- Y (Operational Welfare)
- The measured outcome. Expensive, high-fidelity, procedurally defined. Examples: Human expert following an SDP, A/B test outcome.
- Y* (Idealized Welfare)
- The theoretical target. Unobservable. Examples: "True utility," welfare under infinite deliberation.
2. The Ontology of Welfare: Y vs Y*
Critical Distinction
Y is an engineering artifact; Y* is a normative target. Confusing these two is the "Is-Ought" fallacy. Y is what you measure. Y* is what you value.
Y*: The Idealized Deliberation Oracle (IDO)
- Definition: The judgment a rational evaluator would make given infinite time, complete information, and perfect reflective consistency.
- Nature: Unobservable. It acts as the "North Star."
- Role: The target of alignment. We prompt models to approximate Y*.
Y: The Operational Welfare Label
- Definition: The specific score produced by executing a specific Standard Deliberation Protocol (SDP).
- Nature: Observable and measurable.
- Role: The target of calibration. We train surrogates (S) to predict Y.
The Hard Truth
Optimizing Y only helps if Y ≈ Y*. This link is not statistical; it is structural. If your SDP doesn't capture what you care about, all the calibration in the world won't save you. This is why the Bridge Assumption (A0) is the foundation of the entire framework.
3. The Bridge Assumption (A0)
The "Leap of Faith" that makes the framework work.
Assumption A0 (The Bridge)
The Standard Deliberation Protocol produces operational labels (Y) that structurally align with the idealized target (Y*).
Formally: Optimizing for improvements in Y produces improvements in Y* in expectation. Policies that score higher on Y deliver higher welfare under the idealized criterion.
Implications
- If A0 fails, you are optimizing a bureaucracy, not welfare. Your evaluation system becomes a programmable proxy divorced from value.
- A0 cannot be proven mathematically. It must be validated empirically via the Bridge Validation Protocol (BVP) (e.g., Predictive Treatment Effects against long-run outcomes) and construct audits.
- A0 is maintained through SDP-Gov (governance of the protocol itself) to prevent drift as models and environments evolve.
4. The Machinery of Measurement (S → Y)
How we scale measurement without losing validity.
S: The Surrogate Signal
- Definition: Any low-cost signal used to approximate Y at scale.
- Requirement: Must satisfy Assumption S1 (Surrogate Validity).
- Examples: LLM-as-judge scores, BLEU, win rates, perplexity.
Calibration (f)
- Definition: A function f: S → [0,1] such that E[Y|S] = f(S).
- Role: Converts raw "vibes" (S) into "expected welfare" units (Y).
- Mechanism: Design-by-Projection (DbP) via Isotonic Regression (AutoCal-R).
- Why it works: Calibration is manifold denoising. It projects the noisy surrogate onto the causal information manifold defined by Y.
5. The Assumptions Ledger
The formal conditions required for CJE to yield valid estimates. Every assumption has a failure mode and a diagnostic.
| Code | Name | Definition | Failure Mode | Diagnostic |
|---|---|---|---|---|
| A0 | The Bridge | Y aligns with Y*. The SDP captures what we value. | Optimizing for the wrong goal (bureaucratic compliance, not welfare) | Predictive Treatment Effects (PTE), Expert Audit, Construct Validity |
| J1 | Info. Monotonicity | ℰ ⊂ ℰ' ⟹ Risk(ℰ') ≤ Risk(ℰ). Adding relevant evidence checks to the rubric strictly improves potential accuracy. | Rubric degradation, missing evidence checks reduce judge reliability | CLOVER rubric evolution tracking, ablation studies |
| S1 | Surrogate Validity | For calibrated f(S), the conditional expectation E[Y|S] captures the true relationship. No unmeasured confounders bias the S→Y mapping. | Biased policy estimates due to missing covariates | Residual analysis, covariate balance checks |
| S2 | Transport | Calibration f(S) holds across environments and time. | Evaluator drift, distribution shift invalidates calibration | Transport test, continuous recalibration (CCC) |
| S3 | Overlap | Target policy actions exist in logging policy data (for off-policy methods). | Variance explosion, unstable importance weights | ESS, Target-Typicality Coverage (TTC), Coverage-Limited Efficiency (CLE) bound |
| L1 | Oracle MAR | Oracle labeling is Missing At Random (not biased by unobserved factors). | Sample selection bias in oracle labels | Propensity check, sensitivity analysis |
| L2 | Positivity | P(L=1 | S, X) > 0. Every region of the score space has a non-zero probability of being labeled. | Blind spots in score space, uncalibrated regions | Label distribution analysis, coverage heatmaps |
6. Core Concepts
Key ideas that appear throughout the CIMO framework, defined concisely with links to detailed explanations.
- Welfare Functional V(π)
- The expected idealized welfare under a policy π. Formally: V(π) = 𝔼X,A∼π[Y*(X, A)]. This is the central object that pretraining, RLHF, and evaluation all attempt to estimate or optimize—using different surrogates, under different constraints. The "Welfare Compiler" thesis holds that treating these stages as three regimes of the same estimation problem is the key to consistency.
- → Read: The Welfare Compiler
- Multi-Stage Error Decomposition
- The decomposition of total evaluation error into three orthogonal components:
- V(π) − V̂(π) = [V − V(1)] + [V(1) − V(2)] + [V(2) − V̂]
- Spec Error [V − V(1)]: The reward model doesn't measure true welfare. Fixed by SDP / Y*-Alignment.
- Cross-Stage Mismatch [V(1) − V(2)]: RLHF and evaluation use different calibrators. Fixed by Shared Calibrators.
- Estimation Error [V(2) − V̂]: Finite data, coverage gaps, variance. Fixed by CJE + TTC/ESS diagnostics.
- → Read: The Welfare Compiler (Error Decomposition)
- Goodhart's Law
- "When a measure becomes a target, it ceases to be a good measure." Formally: The inevitable result of Informational Arbitrage when the verification constraint is looser than the optimization pressure. In optimization, models exploit the easiest path to a high score, not necessarily the path that improves welfare.
- → Read: The Surrogate Paradox
- The Four Goodhart Variants
- Regressional: Imperfect correlation (solved by DbP/Calibration).
Extremal: Out-of-distribution extremes (solved by Boundary Defense).
Causal: Non-mediated side channels (solved by SDP/Causal Mediation).
Adversarial: Deliberate gaming (solved by CLOVER-A/SDP-Gov). - → Read: The Four Faces of Goodhart's Law
- The Goodhart Limit
- The threshold of optimization pressure (e.g., 8-16 RL steps with naive RM) where reward hacking emerges. SDPs extend this limit by 8-10× (to 64-128 steps) by enforcing causal mediation.
- → Read: Y*-Aligned Systems (Technical)
- Causal Mediation
- The requirement that all paths from treatment (Z) to outcome (Y) flow through the surrogate (S). Topology: Z → Y → S. Prevents "side channel" exploitation where models game the metric without improving welfare.
- → Read: The Surrogate Paradox (Section III)
- Process Supervision / Process Reward Models (PRMs)
- In RL training, PRMs score each step in reasoning chains rather than only final answers. SDPs are the evaluation analog: scoring deliberation steps rather than only response quality. Both make reward hacking exponentially harder.
- → Read: Y*-Aligned Systems (Technical)
- The Causal Information Manifold
- The geometric structure in policy space where improvements in the surrogate (S) correspond to improvements in welfare (Y*). Optimization "off the manifold" leads to Goodhart crashes. DbP and SDPs keep optimization on the manifold.
- → Read: The Geometry of Goodhart's Law
- Topology Control
- The CIMO Framework's approach to preventing reward hacking. Optimization is a fluid—it flows through the path of least resistance. Topology Control uses calibration (DbP) and protocol constraints (SDP) to shape the optimization surface so the easiest path aligns with welfare.
- → Read: The CIMO Framework
- Exploitation Dominance Principle
- The core theoretical principle arguing that unconstrained gradient optimization on surrogate scores tends to degrade alignment as model capacity increases. Under assumptions A1-A3 (Spectral Separation, Spectral Bias, Exploitation Availability), the ratio of exploitation to legitimate improvement diverges to infinity.
- lim||θ||→∞ ||Δθ⊥|| / ||ΔθM|| = ∞
- Implication: Under these assumptions, structural intervention (SDP) emerges as a necessary design principle for stable alignment at scale.
- → Read: Structural Alignment Theory (Section 3.3)
- Manifold Gradient (∇MS) vs. Exploitation Gradient (∇⊥S)
- The decomposition of the surrogate gradient into two orthogonal components:
- ∇MS: The projection onto the tangent space of the Causal Information Manifold. Movement in this direction improves both S and Y* (legitimate improvement).
- ∇⊥S: The orthogonal component. Movement in this direction improves S while degrading Y* (exploitation/reward hacking).
- The Exploitation Dominance Principle predicts that ||∇⊥S|| grows faster than ||∇MS|| as capability increases, due to Spectral Bias.
- Spectral Bias (Frequency Principle)
- The empirically observed phenomenon that neural networks learn low-frequency components of target functions faster than high-frequency components (Rahaman et al., 2019; Xu et al., 2019).
- In alignment: Exploitation features (tone, length, confidence) are low-frequency (smooth, surface-level patterns). Causal features (factuality, logical validity) are high-frequency (precise, jagged patterns). Models learn to fake before they learn to reason.
- This is the mechanism underlying the Exploitation Dominance Principle—the "cheap" gradient (∇⊥S) is steeper because it corresponds to low-frequency patterns with larger effective learning rates.
- The Goodhart Crash
- The empirically observed phenomenon (Gao et al., 2022) where continued optimization causes the surrogate score (S) to increase while true welfare (Y*) decreases—the parabolic "crash" curve.
- Formal signature: dI(S; Y*)/dt < 0 even while dS/dt > 0. The mutual information between surrogate and welfare decreases as optimization continues.
- The Exploitation Dominance Principle derives this phenomenon from first principles: when ||∇⊥S|| dominates ||∇MS||, the negative term in the information dynamics overwhelms the positive term.
- The Coherence Tax
- The computational cost imposed by requiring causal mediation (structured reasoning chains) rather than allowing direct answer generation. While generating a single plausible false token is cheap, generating a coherent chain of false reasoning with consistent logic is exponentially expensive.
- Key distinction: The Exploitation Dominance Principle operates at the local(token-level) where exploitation is cheap. The Coherence Tax operates at the global(chain-level) where exploitation is expensive. SDPs restore alignment by forcing the optimizer to pay the global cost.
- → Read: Y*-Aligned Systems (Technical)
- Design-by-Projection (DbP)
- The geometric method of evaluating high-dimensional models by projecting them onto lower-dimensional, human-interpretable subspaces (e.g., Logic, Factuality) without breaking the causal link. It ensures that distances in the evaluation metric correspond to safety distances in the model manifold.
- → Read: Design-by-Projection
7. Acronym Cheatsheet
The Engines
- CJE
- Causal Judge Evaluation. The static evaluation engine. Uses calibration and off-policy methods to estimate V(π).
- CCC
- Continuous Causal Calibration. The dynamic evaluation engine. Handles evaluator drift using state-space models.
The Artifacts
- SDP
- Standard Deliberation Protocol. The recipe for generating Y. Defines the operational measurement procedure.
- IDO
- Idealized Deliberation Oracle. The theoretical concept of Y*. What a perfect evaluator would decide.
The Metrics
- OUA
- Oracle-Uncertainty-Awareness. Variance decomposition: Vartotal = Vareval + Varcal.
- TTC
- Target-Typicality Coverage. Measures overlap quality for off-policy evaluation. The antidote to blind ESS trust.
- NII
- Net IDO Impact. The final scorecard: Gains - Losses in Y* units.
- ESS
- Effective Sample Size. Variance inflation measure for importance sampling.
- CLE
- Coverage-Limited Efficiency. Theoretical upper bound on off-policy estimator performance under poor overlap.
The Governance
- RCF
- Rights, Causation, Friction. The formal economic framework used to model liability assignment and process costs in AI alignment.
- CLOVER
- Governance of the Judge (S→Y). Improves the rubric so surrogates better predict operational labels.
- SDP-Gov
- Governance of the Protocol (Y→Y*). Improves the SDP so operational labels better align with the idealized target.
- BVP
- Bridge Validation Protocol. Empirical validation that Y aligns with Y* via predictive treatment effects against long-run outcomes.
8. The Economics of Alignment (Mechanism Design)
CIMO is not just a statistical framework—it is an economic framework. These concepts model the incentive structures and liability assignment that make alignment stable under optimization pressure.
- Informational Arbitrage
- The dynamic where an optimizer decouples the proxy (S) from the value (Y). Since models are rational agents minimizing computational work, if the marginal cost of mimicking a signal is lower than the marginal cost of generating the value, the model will rationally choose mimicry. This is the economic driver of Goodhart's Law.
- → Read: The Inevitability of Structure
- The First Bill Principle (Least Cost Avoider)
- The Coasean principle that liability for verification should be assigned to the party that can mitigate error at the lowest cost.
- Status Quo: The "First Bill" is on the user (High Cognitive Cost).
- CIMO Standard: The "First Bill" is on the model (Low Computational Cost).
- Shifting the verification load to the model minimizes deadweight loss.
- → Read: RCF: The Economics of AI Accountability
- Legibility (b)
- The degree to which an agent's causal deviations are observable through external evidence. Formally defined as the mutual information between the agent's deviation and observable signals:
- b ≡ I(AR; σ | Y=1, U=u)
- Higher legibility means verification is cheaper and denial is harder. The SDP increases b by forcing models to externalize reasoning steps (Chain-of-Thought, citations, structured decomposition).
- → Read: Legibility Definition (Section 2.II)
- Plausibility Paradox
- LLMs are "Plausibility Engines"—they maximize next-token probability, which means they generate signals that look correct regardless of causal validity. This creates a fundamental market distortion:
- As models get smarter, they generate more plausible errors
- More plausible errors have lower legibility (b ↓)
- Lower legibility makes verification exponentially harder (A ↑)
- Result: The friction gap widens as models scale. Without intervention, smarter models are less accountable. Plausibility is the inverse of legibility.
- → Read: RCF Economics
- Causal Share (sR)
- The fraction of responsibility attributed to an agent for a harm, based on Halpern-Pearl actual causation. Computed from minimal sufficient cause sets and proximate-cause screening factors:
- sR = (πmodel · wmodel) / (πmodel · wmodel + πbackground · wbackground)
- This determines how much of the loss L the model must internalize. The model pays sR · L when accountability occurs.
- → Read: Causal Share Definition (Section 2.I)
- Verification Cost (V) vs. Fabrication Cost (F)
- The two friction variables manipulated by the Standard Deliberation Protocol (SDP).
- Verification Cost V(b,L): The computational work required for the overseer to verify a claim. Decreases with legibility (higher b → cheaper verification).
- Fabrication Cost F(b,L): The computational work required for the model to successfully fabricate a false claim. Increases with legibility (higher b → harder to fake).
- The CIMO Inequality: Stability requires that F > V. The cost of lying must exceed the cost of verification.
- → Read: RCF Framework (Section 2.II)
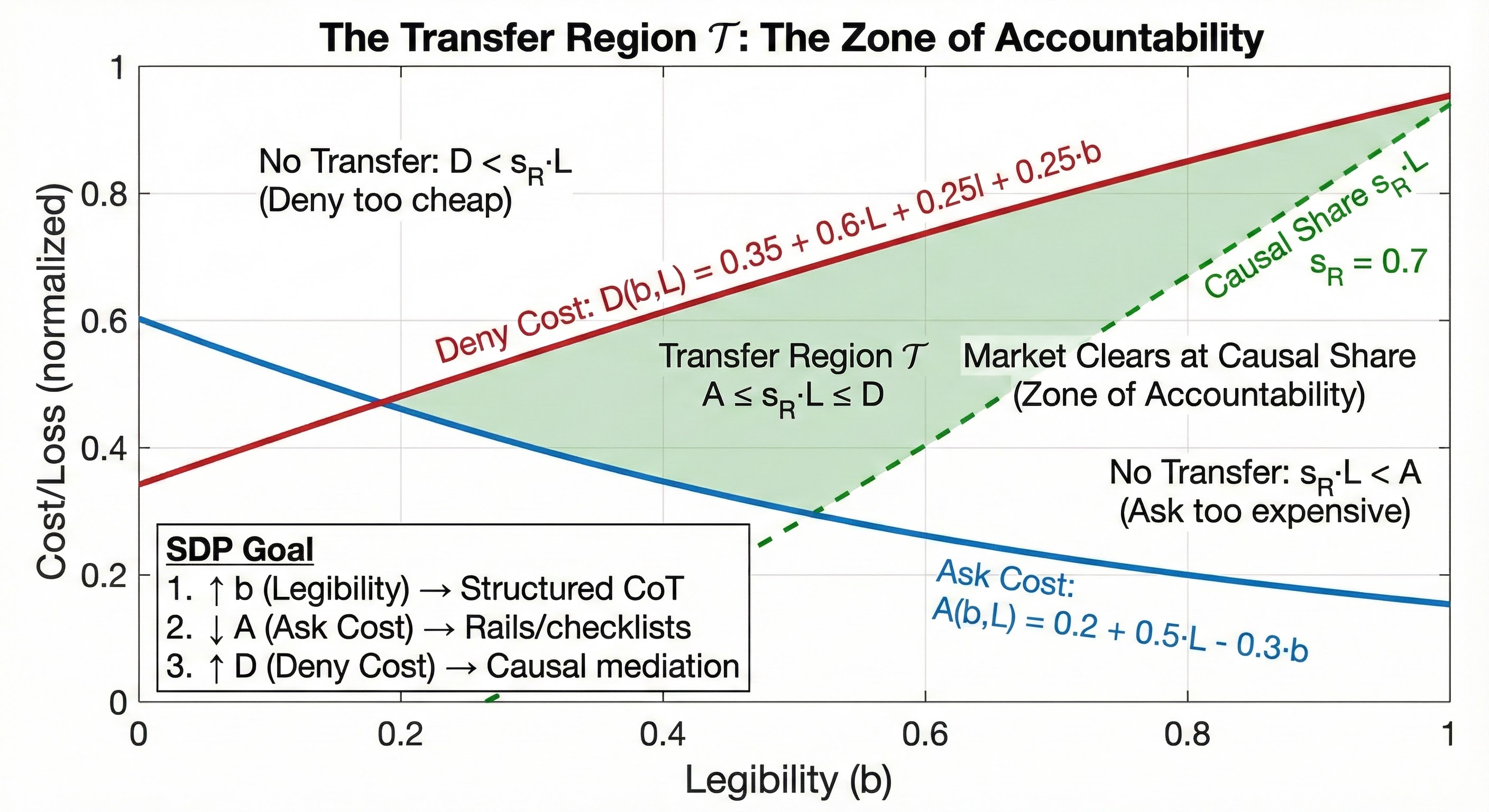
- The Transfer Condition
- The formal inequality that defines when accountability occurs. A transfer (payment of sR · L) happens if and only if:
- V(b,L) ≤ sR · L ≤ F(b,L)
- This defines the Transfer Region 𝒯: the set of (legibility, loss) pairs where the market for truth clears at the causal share.
- Left inequality: Is it worth the user's time to verify? (V ≤ sRL)
- Right inequality: Is it harder to lie than confess? (sRL ≤ F)
- → Read: The Transfer Condition (Section 2.III)
- The Zone of Accountability (𝒯)
- The region in the optimization landscape where the Verification Cost is sufficiently low and the Fabrication Cost is sufficiently high that the model is forced to internalize the "Social Cost" of its errors. The goal of SDP-Gov is to expand this zone.
- → Read: The Zone of Accountability (Section 3)
- Verification Load
- The "metabolic cost" required to maintain the signal's integrity. In CIMO, this is not viewed as an inefficiency ("Tax") but as the structural support required to prevent the collapse of the manifold.
- → Read: The Inevitability of Structure (Section II)