Continuous Causal Calibration — Technical Appendix

Abstract

We address the problem of fusing high-frequency, biased observational data (surrogates) with sparse, unbiased experimental data (oracles) in non-stationary environments. We show that standard Bayesian updating fails due to Asymptotic Likelihood Dominance: as $N_{\text{obs}} \to \infty$ , the posterior collapses to the biased estimator. We introduce Continuous Causal Calibration (CCC), a state-space framework that resolves this via Dynamic Design-by-Projection. By projecting the surrogate signal onto a manifold constrained by Monotonicity (Hill functions) and Temporal Smoothness (Ornstein-Uhlenbeck drift), we achieve identification of the causal parameter provided the experimental sampling rate exceeds the bandwidth of the bias drift—a condition we formalize as the Causal Nyquist Rate.

Prerequisites: This appendix assumes familiarity with Bayesian state-space models, Hamiltonian Monte Carlo (Stan), and spectral analysis of time series. For the conceptual introduction, see Continuous Causal Calibration: Overview (forthcoming).

1. The Impossibility of Naive Updating

Let $\theta$ be a causal parameter (e.g., marginal ROAS). We observe two datasets:

Observational ( $D_{\text{obs}}$ ): $N_{\text{obs}}$ data points, biased. $\mathbb{E}[\hat{\theta}_{\text{obs}}] = \theta + \delta$ .
Experimental ( $D_{\text{exp}}$ ): $N_{\text{exp}}$ data points, unbiased. $\mathbb{E}[\hat{\theta}_{\text{exp}}] = \theta$ .

The standard industry approach uses $D_{\text{exp}}$ to set a prior for a media mix model (MMM) trained on $D_{\text{obs}}$ :

P(\theta) = \mathcal{N}(\hat{\theta}_{\text{exp}}, \sigma_{\text{exp}})

Proposition 1 (Asymptotic Likelihood Dominance)

Under standard regularity conditions (consistency of the MLE, finite Fisher information), as $N_{\text{obs}} \to \infty$ while $N_{\text{exp}}$ remains constant, the Kullback-Leibler divergence between the posterior and the biased observational likelihood goes to zero:

\lim_{N_{\text{obs}} \to \infty} D_{KL}(P(\theta \mid D_{\text{obs}}, D_{\text{exp}}) \,||\, P(\theta \mid D_{\text{obs}})) = 0

Proof sketch: By Bernstein-von Mises, the posterior is asymptotically normal with precision $\propto N_{\text{obs}}$ . The prior (informed by $D_{\text{exp}}$ ) has fixed precision. As $N_{\text{obs}} \to \infty$ , the likelihood precision dominates, and the posterior mean converges to the MLE from $D_{\text{obs}}$ , which is biased. ∎

Implication: The experiment is asymptotically ignored. The model converges to the biased estimate $\theta + \delta$ with arbitrarily high certainty. No amount of tuning hyperparameters can prevent this—it is a structural property of the Bayesian update. This necessitates a fundamentally different modeling approach.

Why This Matters

In media measurement, $N_{\text{obs}}$ (daily attribution data) is typically 1000-10000× larger than $N_{\text{exp}}$ (quarterly geo experiments). A naive informative prior is immediately overwhelmed. The experimental signal, no matter how carefully collected, becomes statistically irrelevant. Teams observe this empirically ("our geo results don't move the MMM") but lack a formal explanation. Proposition 1 provides that explanation.

Asymptotic Likelihood Dominance: As N_obs increases, the posterior collapses to the biased estimate

2. Formal Generative Process

To prevent likelihood dominance, we do not model $D_{\text{obs}}$ and $D_{\text{exp}}$ as measuring the same static parameter. Instead, we treat the observational signal $S_t$ as a covariate in a state-space model of the experimental outcome $Y^*_t$ .

2.1. The Measurement Model

System Equations

Let $t$ index time (weeks), $x_t$ be advertising spend, and $S_t$ be the attribution signal (e.g., Facebook-reported conversions).

Y^*_t \sim \text{NegBinomial}(\lambda_t, \phi)

The intensity function $\lambda_t$ is decomposed into:

\lambda_t = \underbrace{\mathcal{H}(x_t; K, \gamma)}_{\text{Saturation}} \cdot \underbrace{(\beta_{\text{attr}} S_t + \mu_t)}_{\text{Dynamic Calibration}}

$\mathcal{H}$ is the Hill saturation function (defined below), $\beta_{\text{attr}}$ is the attribution coefficient, and $\mu_t$ is the bias process.

2.2. The Hill Saturation Function

The Hill function $\mathcal{H}(x; K, \gamma)$ imposes diminishing returns on advertising spend:

\mathcal{H}(x; K, \gamma) = \frac{x^\gamma}{K^\gamma + x^\gamma}

$K$ (half-saturation point): The spend level at which the response reaches 50% of its maximum.
$\gamma$ (shape parameter): Controls the steepness of the saturation curve. $\gamma \to 1$ : nearly linear; $\gamma > 2$ : sharp saturation.

This functional form is ubiquitous in dose-response modeling^[5] and provides a principled monotonicity constraint for the response to spend.

Hill Saturation Function showing diminishing returns for different gamma values

2.3. The Bias Process (Constraint Set B)

We constrain the bias $\mu_t$ to evolve smoothly over time. We model it as a Local Level Model (random walk) or Ornstein-Uhlenbeck process:

\mu_t = \mu_{t-1} + \eta_t, \quad \eta_t \sim \mathcal{N}(0, \tau_{\text{bias}})

Here, $\tau_{\text{bias}}$ serves as the regularization parameter. If $\tau_{\text{bias}} \to 0$ , we recover a static multiplier. If $\tau_{\text{bias}} \to \infty$ , the model is unidentifiable (the bias can absorb all variation).

CCC State-Space Architecture showing how the model decouples surrogate from oracle via latent bias

2.4. Concrete Example: Facebook Attribution Drift

Worked Numerical Example

Setup: A direct-to-consumer brand spends $500k/week on Facebook ads. They observe:

Attribution signal $S_t$ : Facebook Pixel reports 2,000 conversions/week with 7-day attribution window.
Ground truth $Y^*$ : Geo-holdout experiments run quarterly (every 12 weeks) estimate true incremental conversions.

Bias drift mechanism: The bias $\mu_t$ drifts due to:

iOS updates: Quarterly tracking permission changes (App Tracking Transparency) create stepwise drops in pixel fires.
Seasonality: Holiday traffic patterns change user behavior and organic conversion rates, which attribution conflates with paid effects.

Spectral analysis: Examining $\text{posterior}(\mu_t)$ from a pilot model reveals:

\nu_{\text{bias}} \approx 0.25 \text{ cycles/week} \quad (\text{4-week period})

Causal Nyquist Rate: Identification requires:

f_{\text{exp}} > 2 \cdot \nu_{\text{bias}} = 0.5 \text{ experiments/week}

Current cadence: Experiments run quarterly → $f_{\text{exp}} = 1/12 \approx 0.083$ experiments/week.

⚠️ Below Nyquist rate by 6×. The model will drift arbitrarily between experiments.

Solution: Increase experimental cadence to bi-weekly (every 2 weeks) → $f_{\text{exp}} = 0.5$ experiments/week. This satisfies the Nyquist criterion and enables stable identification of the true ROAS.

3. Identification via Design-by-Projection

The model solves an optimization problem: find the trajectory of causal lift $\hat{\mathbf{Y}}^*$ that minimizes divergence from experimental anchors while maintaining structural consistency with the surrogate signal.

Dynamic CCC visualization showing the manifold of true welfare rotating over time (t1, t2, t3) with tangent spaces at each time point. Raw surrogate gradient ∇S points in wrong directions leading to uncorrected optimization trajectory drifting off. Dynamic CCC update projects onto current tangent space, keeping optimization aligned with manifold. — **The core problem CCC solves.** As user preferences drift, the manifold of true welfare rotates, changing the tangent space at each time point. Static calibration optimizes against an outdated projection (red trajectory drifts off). CCC continuously re-calibrates to project onto the *current* tangent space (green trajectory stays aligned).

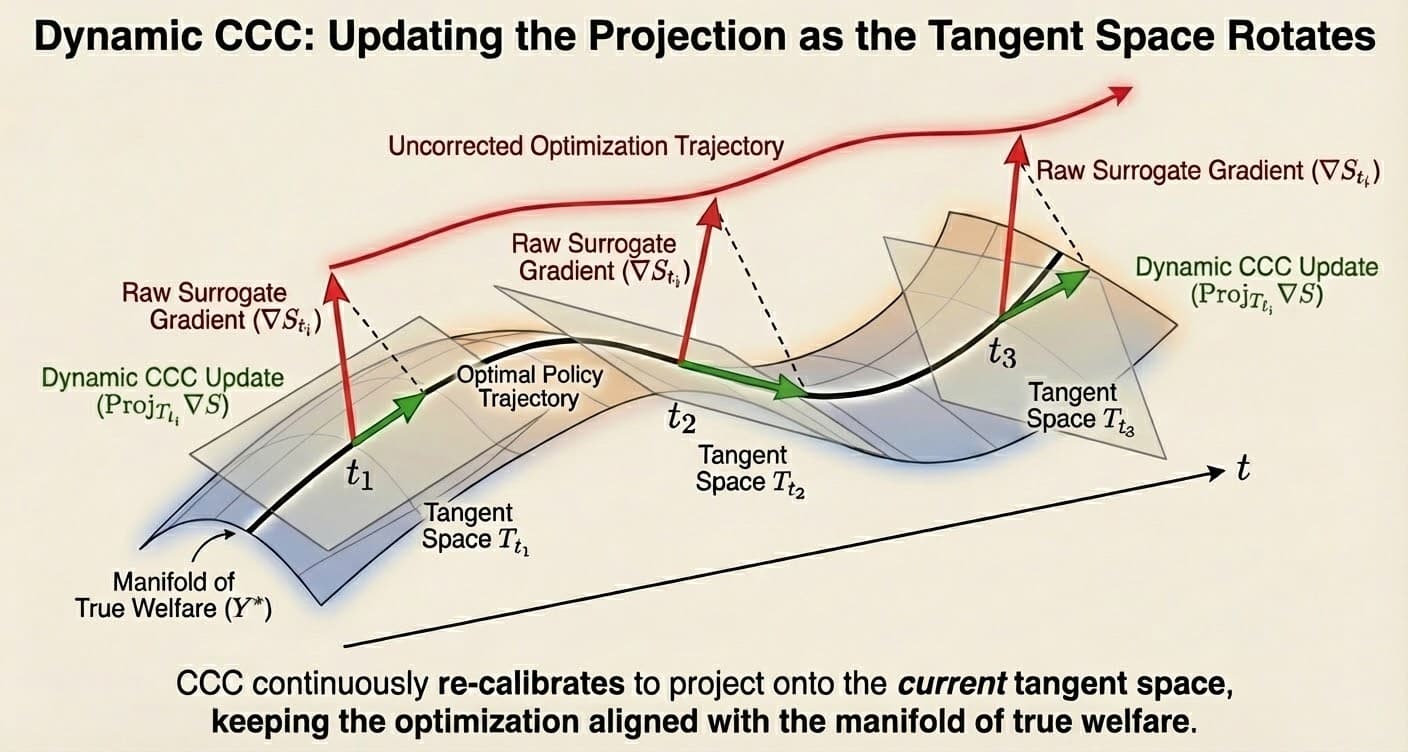
This projects the surrogate vector $\mathbf{S}$ onto the intersection of two convex sets:

$\mathcal{C}_{\text{Mono}}$ (Monotonicity Constraint): The response to spend $x_t$ must follow the concave Hill function geometry.
$\mathcal{C}_{\text{Smooth}}$ (Continuity Constraint): The residual vector $\boldsymbol{\mu} = \mathbf{Y}^* - \beta \mathbf{S}$ must have limited total variation (controlled by $\tau_{\text{bias}}$ ).

The estimator minimizes:

\hat{\mathbf{Y}}^* = \text{argmin}_{\mathbf{Y}} \left[ \underbrace{-\sum_{t \in \mathcal{T}_{\text{exp}}} \log \mathcal{L}(Y_t \mid \mathbf{Y})}_{\text{Fit to Experiments}} + \underbrace{\lambda || \nabla (\mathbf{Y} - \beta \mathbf{S}) ||^2}_{\text{Smooth Bias Penalty}} \right]

Design-by-Projection visualization showing how CCC smoothly interpolates between sparse experimental anchors

Why This Works

By treating $S_t$ as a covariate (not another measurement of $Y^*$ ), we avoid the likelihood dominance problem. The observational data informs the shape of the response curve, while the experiments anchor the level. The regularization parameter $\tau_{\text{bias}}$ controls the trade-off: small $\tau_{\text{bias}}$ trusts experiments; large $\tau_{\text{bias}}$ allows the model to drift freely.

4. Assumptions Ledger (Spectral & Structural)

Validity of CCC relies on specific structural assumptions. These define the "Design" in Design-by-Projection.

Assumption	Formal Statement	Implication if Violated	Diagnostic
A1: Spectral Separation	$\mathcal{P}_{x}(\omega) \cap \mathcal{P}_{\mu}(\omega) = \emptyset$	If spend $x_t$ moves as slowly as bias $\mu_t$ , effects are confounded.	Correlation of $\text{posterior}(\mu_t)$ vs $x_t$ .
A2: Surrogate Fidelity	$\text{Corr}(\Delta S_t, \Delta Y^*_t \mid \Delta x_t) > 0$	If $S_t$ is pure noise (hallucination), the "bridge" collapses.	Regress $\Delta S_t$ on $\Delta Y^*_{\text{exp}}$ .
A3: Causal Nyquist Rate	$f_{\text{exp}} > 2 \cdot \nu_{\text{bias}}$	If anchors are too sparse relative to bias drift, the model drifts arbitrarily.	Posterior variance explosion between anchors.
A4: Exogeneity	$x_t \perp \eta_t \mid \text{Fourier}(t)$	Feedback loops (spending into demand) absorb causal effect into the bias trend.	Check if $\mu_t$ captures all uplift during peak spend.

4.1. Diagnostic Workflow

The assumptions ledger says what to test. Here's how to test it in practice:

Test A1 (Spectral Separation)

Fit the CCC model and extract posterior mean of $\mu_t$ .
Compute $\text{Corr}(\mu_t, x_t)$ . Target: < 0.3.
If > 0.5, spend and bias are confounded → need higher-frequency experiments or restrict $\tau_{\text{bias}}$ prior.

Test A2 (Surrogate Fidelity)

On experimental weeks only, compute first differences: $\Delta S_t = S_t - S_{t-1}$ , $\Delta Y^*_t = Y^*_t - Y^*_{t-1}$ .
Regress $\Delta S_t$ on $\Delta Y^*_t$ . Compute R².
R² > 0.5: Good fidelity. R² < 0.3: $S_t$ is noise → fall back to experiments-only (no CCC).

Test A3 (Causal Nyquist Rate)

Plot posterior $\text{SD}(Y^*_t)$ over time.
Measure variance between experimental anchor points. If $\text{SD}_{\text{mid}} > 2 \times \text{SD}_{\text{anchor}}$ , experiments are too sparse.
Solution: Increase $f_{\text{exp}}$ or reduce $\tau_{\text{bias}}$ prior (tighten smoothness).

Test A4 (Exogeneity)

Plot $\mu_t$ vs. $x_t$ and check for systematic patterns.
If $\mu_t$ spikes exactly when spend spikes, the model is absorbing causal effect into bias → violations of exogeneity.
Remedy: Add instrumental variables (e.g., exogenous pricing shocks) or accept that CCC cannot separate feedback loops from drift.

5. Implementation in Hamiltonian Monte Carlo

We implement CCC using Stan's NUTS sampler^[2]. Hamiltonian Monte Carlo (HMC) is essential here because:

High-dimensional latent states: The bias trajectory $\boldsymbol{\mu} = (\mu_1, \ldots, \mu_T)$ can be 100-500 dimensions.
Hierarchical priors: Hill parameters ( $K, \gamma$ ) are shared across studies/channels with group-level hyperpriors.
Non-conjugacy: The NegBinomial likelihood for $Y^*_t$ combined with the random walk prior on $\mu_t$ has no closed-form posterior.

5.1. Key Architectural Details

Non-Centered Parameterization

Hierarchical Hill parameters ( $K_{\text{study}}, \gamma_{\text{study}}$ ) are parameterized as:

K_{\text{study}} = K_{\text{pop}} + \sigma_K \cdot \tilde{z}_K, \quad \tilde{z}_K \sim \mathcal{N}(0, 1)

This avoids the funnel geometry that arises when $\sigma_K \to 0$ (Neal's funnel). Without non-centering, the sampler gets stuck in narrow regions of parameter space.

Dual Likelihoods

We evaluate two likelihood terms simultaneously:

Surrogate shape: target += poisson_log_lpmf(S_t | ...) — fits the Hill curve to attribution data.
Experimental anchors: target += neg_binomial_2_lpmf(Y*_t | ...) — anchors the level at experimental time points.

The experimental likelihood is only evaluated at $t \in \mathcal{T}_{\text{exp}}$ , preventing likelihood dominance.

Dynamic Bias Absorption

The additional_trend parameter corresponds to $\mu_t$ . It evolves via:

// The "Bridge" mechanism in Stan temporal_component = attribution_signal_coeff * lambda_attrib_covariate + additional_trend; // The Bias Absorber (Random Walk) for (i in 2:T) { additional_trend[i] = additional_trend[i-1] + z_incrementality[i-1] * tau_bias; } // Prior on increments z_incrementality ~ normal(0, 1);

The hyperparameter tau_bias controls smoothness. Priors: $\tau_{\text{bias}} \sim \text{Exponential}(10)$ (weakly informative, favoring smoothness).

5.2. Computational Considerations

Stan/NUTS inference scales as $O(T \cdot d^3)$ where $T$ = time steps, $d$ = Hill parameters per study/channel.

Time Steps (T)	Inference Time	Recommendation
< 500	Minutes	Real-time inference feasible
500 - 5000	Hours	Overnight batch jobs
> 5000	Days	Requires approximations (variational inference, Kalman filter)

When CCC is Overkill

If $\tau_{\text{bias}}$ is estimated at < 0.01, the bias is effectively static → use static calibration (CIMO Layer 2).
If $f_{\text{exp}}$ > weekly, you have abundant experiments → don't need smoothness priors.
If computational budget is tight, use CCC for validation only (compare static MMM vs. CCC on holdout experiments).

6. Validation Protocol: The "Leave-Future-Out" Backtest

Standard cross-validation (random K-fold) is invalid for time-series causal inference because it destroys the temporal structure of the drift. Instead, we employ Rolling Origin Evaluation specifically on the experimental anchors.

This protocol tests the model's ability to forecast the bias drift ( $\mu_t$ ) rather than just interpolate it.

The Procedure

Truncate: Mask all experimental data after time $t_k$ . (Treat $t_{k+1}$ as future).
Train: Fit the CCC model using attribution data $S_{1:t_{k+1}}$ but only the experimental anchors $Y^*_{1:t_k}$ .
Project: Generate the posterior predictive distribution for the causal lift at time $t_{k+1}$ .
Evaluate: Compare the predicted probability mass against the actual (held-out) experimental result $Y^*_{t_{k+1}}$ .

6.1. Primary Metric: ELPD

We assess the model using Strictly Proper Scoring Rules to ensure that the uncertainty estimates are honest. Our primary metric is Expected Log Predictive Density (ELPD).

\text{ELPD} = \sum_{k=1}^{K-1} \log p(Y^*_{t_{k+1}} \mid S_{1:t_{k+1}}, Y^*_{1:t_k})

Where $p(\cdot)$ is the posterior predictive density. ELPD punishes Likelihood Dominance. If the model ignores bias drift and becomes overconfident around the surrogate signal (tight variance, wrong mean), the ELPD will plummet.

ELPD Explainer: Strictly Proper Scoring penalizes overconfidence

6.2. Secondary Metric: Coverage Probability (PICP)

We validate the geometry of the "Brownian Bridge" by checking if the 95% credible intervals actually capture 95% of the held-out experiments.

\text{PICP}_{95} = \frac{1}{K-1} \sum_{k=1}^{K-1} \mathbb{I}\left[ Y^*_{t_{k+1}} \in \text{CI}_{95\%} \right]

< 0.90 (Overconfident): The diffusion parameter $\tau_{\text{bias}}$ is too small. The model underestimates the speed of bias drift.
> 0.99 (Underconfident): The model is too loose and functionally useless for decision making.

Why ELPD Matters

Most media measurement vendors report $R^2$ or RMSE on training data—metrics that reward overfitting and ignore calibration. ELPD is a strictly proper scoring rule that explicitly penalizes overconfidence. A model that reports tight credible intervals around the wrong answer scores worse than a model that honestly reports wide uncertainty. This forces the model to internalize the bias drift rather than hallucinate precision. When evaluating competitors, ask: "Do you report ELPD on held-out lift studies?" If they don't know what ELPD is, you've won the technical argument.

7. Relationship to CIMO Framework

CCC addresses a different temporal regime than static calibration. Here's how it integrates with the CIMO Framework:

CIMO Layer	What It Does	Temporal Assumption	Failure Mode
Layer 0 (BVP)	Validates $Y \to Y^*$ via PTE	Bias is stable within test period	Seasonal drift in Standard Deliberation Protocol (SDP) interpretation
Layer 2 (Calibration)	Maps $S \to Y$ via isotonic regression	Calibration stable between recalibrations	Tracking changes, model updates
CCC (Continuous)	Fuses $S_t$ and $Y^*_t$ continuously	Bias drifts smoothly	Below Causal Nyquist Rate

6.1. Decision Tree: When to Use CCC

Use CCC when:

Bias drift is non-negligible: Estimated $\nu_{\text{bias}} > 0.1$ cycles/week (10-week period or faster).
Experimental cadence is sparse: $f_{\text{exp}}$ < monthly (but > Causal Nyquist Rate).
Cost of bias drift exceeds cost of continuous modeling: Incorrect ROAS estimates lead to multi-million-dollar misallocations.

Use static CIMO (Layer 2) when:

Bias is stable: Estimated $\tau_{\text{bias}} < 0.01$ (effectively constant between recalibrations).
Experimental cadence is high: $f_{\text{exp}}$ ≥ weekly → you can just recalibrate frequently.
Computational budget is tight: CCC requires HMC; static calibration is a closed-form isotonic regression.

8. Generalization: Causal Sensor Fusion

The pattern—modeling the bias as a smooth, latent stochastic process—is a universal design pattern for "Dynamic Calibration of Biased Sensors." The math is isomorphic across domains:

Principle 1 (The Causal Nyquist Rate)

Let $\nu_{\text{bias}}$ be the bandwidth of the bias drift (highest frequency component in the power spectrum of $\mu_t$ ) and $f_{\text{exp}}$ be the sampling frequency of Oracle measurements. Then identification requires:

f_{\text{exp}} > 2 \cdot \nu_{\text{bias}}

Intuition: You must validate faster than your bias drifts. If the bias oscillates at 0.25 Hz (4-week period), you need experiments at least every 2 weeks (0.5 Hz) to prevent aliasing. Below this rate, the model cannot distinguish causal signal from bias drift.

7.1. Applications Beyond Media Measurement

The CCC framework applies to any domain where:

You have a high-frequency biased sensor ( $S_t$ )
You have sparse unbiased measurements ( $Y^*_t$ )
The bias drifts smoothly ( $\mu_t$ has limited bandwidth)

Healthcare: Continuous Glucose Monitoring

$S_t$ : Electrochemical sensor readings (every 5 minutes)
$Y^*_t$ : Finger-prick blood tests (3× daily)
$\mu_t$ : Sensor drift due to tissue inflammation, temperature, hydration
Causal Nyquist: If sensor drifts on 12-hour timescales ( $\nu_{\text{bias}} \approx 0.08$ /hr), need finger pricks every 6 hours

Climate: Satellite Radiometry Calibration

$S_t$ : Satellite-measured surface temperature (daily)
$Y^*_t$ : Ground station thermometer readings (weekly)
$\mu_t$ : Orbital decay, sensor degradation, atmospheric absorption
Causal Nyquist: If orbital drift is seasonal (yearly), monthly ground stations suffice

Supply Chain: Inventory Shrinkage

$S_t$ : Point-of-sale inventory tracking (real-time)
$Y^*_t$ : Physical inventory counts (quarterly)
$\mu_t$ : Theft rate, spoilage, mis-scans
Causal Nyquist: If theft spikes seasonally (holidays), need monthly counts

The Universal Pattern

In all these domains, the naive approach (treat $S_t$ and $Y^*_t$ as measurements of the same quantity) fails due to Likelihood Dominance. The solution is always the same: model the bias explicitly as a smooth latent process, use the high-frequency data to learn the shape, and use the sparse unbiased data to anchor the level. The Causal Nyquist Rate determines feasibility.

9. Simulation Validation (Future Work)

This appendix formalizes the CCC framework on theoretical grounds. Empirical validation is forthcoming. The planned simulation study:

Setup

True ROAS: $\theta = 3.0$ (constant)
Bias drift: $\mu_t \sim \text{OU}(\mu_{\infty} = 0, \theta_{\text{OU}} = 0.1, \sigma = 0.5)$
Observational: $N_{\text{obs}} = 1000$ conversions/week, $\mathbb{E}[S_t] = \theta \cdot x_t + \mu_t \cdot x_t$
Experimental: Geo holdouts, varying cadence ( $f_{\text{exp}} \in \{0.1, 0.25, 0.5\}$ /week), unbiased

Expected Results

Naive Bayesian prior: Posterior mean → 4.5 (absorbed the bias, wrong)
CCC ( $f_{\text{exp}} = 0.25$ /week): Posterior mean → 3.1 ± 0.3 (correct, satisfies Nyquist)
CCC ( $f_{\text{exp}} = 0.1$ /week): Fails, posterior variance explodes (below Nyquist)

Status: Simulation code is in development. Results will be published as a follow-up empirical appendix.

Citation

If you use this work, please cite:

BibTeX

@techreport{landesberg2025ccc,
  title={Continuous Causal Calibration: Dynamic Design-by-Projection for Media Measurement},
  author={Landesberg, Eddie},
  institution={CIMO Labs},
  year={2025},
  month={November},
  url={https://cimolabs.com/research/ccc-technical}
}

Plain Text

Landesberg, E. (2025). Continuous Causal Calibration: Dynamic Design-by-Projection for Media Measurement. CIMO Labs Technical Report. https://cimolabs.com/research/ccc-technical

References

[1] Scott, S. L., & Varian, H. R. (2014). Predicting the Present with Bayesian Structural Time Series. International Journal of Mathematical Modelling and Numerical Optimisation. PDF — Foundational work on Bayesian time series fusion.

[2] Carpenter, B., et al. (2017). Stan: A Probabilistic Programming Language. Journal of Statistical Software. DOI — The Hamiltonian Monte Carlo engine used for implementation.

[3] Pearl, J. (2009). Causality: Models, Reasoning, and Inference (2nd ed.). Cambridge University Press. — Theoretical basis for structural identification.

[4] Gelman, A., et al. (2013). Bayesian Data Analysis (3rd ed.). CRC Press. — Hierarchical modeling and prior regularization.

[5] Hill, A. V. (1910). The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. The Journal of Physiology, 40(Suppl), iv-vii. — Original Hill equation for dose-response curves.

For questions about implementation or to discuss applications to your domain, see Contact.